Estimado alumno Sanjuanista muy buen día les escribe su estimado teacher Dante deseando que te encuentren bien con la bendición de Dios, he preparado un material didáctico que contiene ejercicios básicos resueltos de álgebra además de ejercicios “espejos” que debes desarrollar con mi ayuda y la orientación que en casa existe.
Mi estimado alumno lee con atención la siguiente información:
Ecuaciones diferenciales en tiempos del coronavirus
Modelo SIRM para epidemias
El modelo SIR es un modelo matemático que plantea con ecuaciones diferenciales cómo se propaga una enfermedad en una población. Utiliza tres variables (en este caso utilizamos cuatro). Tenemos a la variable 
que nos indica la cantidad de individuos susceptible, a la variable 
que nos indica la cantidad de individuos infectados y la variable 
que nos dice cuántos recuperados hay. Nosotros agregamos la variable 
para estimar la cantidad de muertos.
que nos indica la cantidad de individuos susceptible, a la variable que nos indica la cantidad de individuos infectados y la variable que nos dice cuántos recuperados hay. Nosotros agregamos la variable 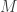para estimar la cantidad de muertos.
La dinámica está descrita por que un infectado puede transmitirle la enfermedad a un susceptible y el infectado puede recuperarse o morir. Así, el modelo de ecuaciones diferenciales que describe a este comportamiento es el siguiente:
Entonces utilizamos los datos oficiales que son publicados en vivo por Plaza Pública para estimar los parámetros 
con 
. Estos se están estimando con el método de mínimos cuadrados.
con . Estos se están estimando con el método de mínimos cuadrados.
Pero para entender estas ecuaciones diferenciales debemos empezar a aprender el siguiente tema:
ECUACIONES DE PRIMER GRADO 0 ECUACIONES LINEALES
Es una igualdad relativa entre dos expresiones matemáticas donde se calcula el valor de la incógnita en función de los demás y a este valor se le denomino solución (raíz) de la ecuación la cual conforma el conjunción solución. Es de 1er grado así se reduce a la forma:
ax + b = 0, donde a es diferente de cero.
A continuación mis estimados estudiantes un video para resolver correctamente las ecuaciones lineales:
Ahora mi estimado alumno a resolver una FICHA para reforzar lo aprendido.
HACER CLICK FICHA
No hay comentarios.:
Publicar un comentario